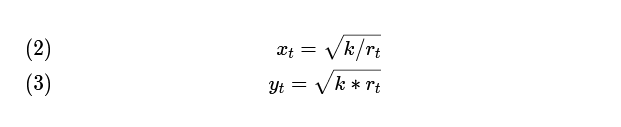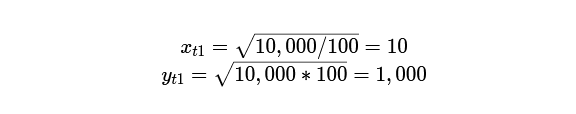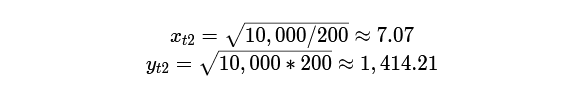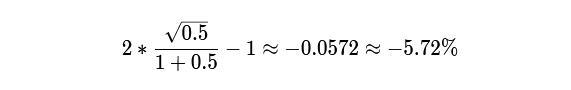Bank of South Korea to change ICO status in cryptocurrency law

ICO

According to an official press release from the Central Bank of South Korea (BOK), the organization has initiated a decision to institutionalize initial coin offerings (ICOs) when adopting a new cryptocurrency law. It has been tentatively named the “Basic Digital Assets Law.”.

Bank officials confirmed that the initiative is indeed being seriously considered by the country’s regulators. South Korea’s Financial Services Commission banned ICOs back in 2017 after the industry’s popularity led to a lot of speculation, fraud and other financial irregularities. BOK noted that the reason for such a decision regarding ICOs was precedents with South Korean projects Paycoin and Terra (LUNA), which legally issued new tokens abroad and then listed them in domestic markets to circumvent the state ban.

The development of the digital asset ecosystem makes it possible to build and use financial services by.

In the first 12 years since Bitcoin’s inception, its value has increased nearly 102.3 million times. In the first.

Beginning in 2017, searches often include queries like “ICO.

The report stated: current legislation and restrictions are ineffective and even hinder the development of the blockchain and crypto sector and technology.

In a report evaluating the European Union (EU) Markets in Crypto Assets Regulation (MiCA), BOK representatives assured that South Korea simply needs to institutionalize ICOs. It is important to make sure that tokens issued outside the country are http://cryptoainews.space/how-to-buy-egod-crypto/ registered and licensed with local regulators. It is mandatory for any cryptocurrency to comply with regulations and trading rules within the state.

In addition, it was stated that there is a need for regulatory measures for stablcoins to protect the interests of national investors.

Earlier edition of Crypto.ru reported: the South Korean authorities decided to tax any free distribution of cryptocurrency tokens, including airdrop and other types.

What are inconsistent losses?

Impermanent Loss, IL) is temporary losses in the process of holding a position on a decentralized exchange based on an automatic market maker (AMM). They are the difference in the value of assets during storage in a wallet (HODL) and holding in a liquidity bullet.

Unstable losses occur mainly in classic pools, where the liquidity provider (Liquidity Provider, LP) should provide both assets in equal ratio, and one of the assets is volatile to the other.

Unstable losses on the example of the DAI/ETH liquidity pool Uniswap, where both tokens are represented in a ratio of 50:50:

We steak in the https://gagarin.news/news/obzor-vast-bank-kak-im-polzovatsya-i-v-cem-ego-osobennosti/ pool 1 ETH and 1000 DAI.
After a week 1 ETH is 2000 DAI.
If we kept 1 ETH and 1000 DAI, then the profit would be 50% (the cost of 1000 DAI would not have changed, but the price of 1 ETH would increase to 2000 DAI).
Steaching tokens in the AMM Pool on Uniswap gives less profit than 50% of simple storage of assets.

Losses are called unstable or unrealized, since they are not fixed until liquidity tokens are removed from the pool. In the example above, if the price of ETH returns to the source 1000 DAI and after that the funds are withdrawn, there are no inconsistent losses.

Uniswap, Sushiswap and similar AMM work in a simple formula:

x ∗ y = k

x – the number of tokens for the asset a;
y – the number of tokens for the asset B;
K – the so -called constant product (Constant Product) of the pool – this value does not change.

The contract retained tokens with an approximate value of $ 153.5 million – 29,116.6 Weth and 76.7 million DAI.

Based on the formula above, we calculate the value K For this, the pool is currently:

29 116.63 ∗ 76 737 921.22 ≈ 2.23 ∗ 10^12

K It only changes when users add or display liquidity, or when a commission is charged from transactions (for example, 0.3% in the case of Uniswap). These funds are added to the total liquidity in the pool.

A detailed example of interaction with the AMM Pool:

Steak 1 ETH and 100 DAI in a pool on Uniswap.
After that, the total liquidity in the bullet is 10 ETH and 1000 DAI (the share of liquidity provider in the pool is 10%).
During the week, transactions for a total of 100 ETH are carried out in the pool (50% in ETH and 50% in DAI), but the price of ETH does not change in relation to DAI.
Within a week, liquidity is not added to the pool and is not excreted from it.
The total liquidity in the pool is now 10.15 ETH and 1015 DAI, taking into account the accumulated commissions at 0.3 ETH.
The share of the liquidity provider in the pool is still 10%, but the steak grew thanks to the commission fee.
If the funds will not derive the funds after a week, there will be no unstable losses, since the price ratio between ETH and DAI remains the same.

Unstable losses in classic pools

An example of a DAI/ETH liquidity pool Uniswap:

We steak 1 ETH and 100 DAI, the share of liquidity provider is 10%.
In the pool 10 ETH and 1000 DAI.
After a week 1 ETH is traded for 200 DAI.
There are no commission fees in the pool.
We calculate inconsistent losses.

First, we calculate K:

k = 10 ∗ 1000 = 10,000

In relation to DAI, the global price of ETH has doubled. Arbitrators took advantage of the opportunity to cheaply redeem it from the pool. Due to increased demand with a limited sentence, price 1 ETH reached 200 DAI.

At the beginning of the week, when 1 ETH cost 100 DAI, there were 10 ETH and 1000 DAI in the pool. We calculate the new distribution of assets in the pool after an increase in the price of ETH. To do this, you need to set several variables, starting with the ratio of prices between assets.

where a and b are two assets in the pool.

In our example a – ETH, B – DAI. 1 ETH first traded for 100 DAI. Therefore, the initial value r equal to 100. We use t, to indicate the time for which it is calculated r.

Combining the above equation with the fundamental formula AMM, you can build formulas for calculating the number of each asset in the pool with any specified ratio r at an arbitrary time t:

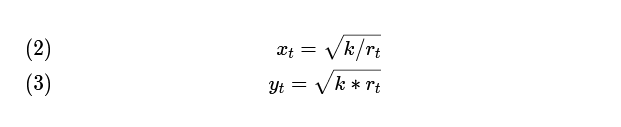
We apply these formulas to the starting position:

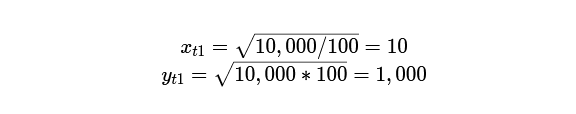
We get the initial state of assets in the pool – 10 ETH and 1000 DAI. Now we apply the same formulas at the end of the example when 1 ETH is traded for 200 DAI. New meaning r equal to 200. We will substitute it into the equations:

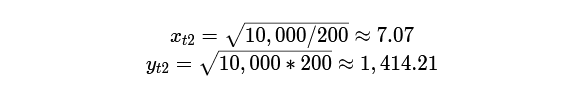
After changing the price of ETH, the pool contains about 7 ETH and about 1414 DAI. You can check the correctness of calculations:

7.07 * 1414.21 ≈ 10,000

The equation of a permanent product remains in force. The share in the pool is 10%, so after changing the price of ETH we have the right to 0.707 ETH and 141.421 DAI.

If assets (1 ETH and 100 DAI) were simply stored on the wallet, their cost would be $ 300. However, the cost of funds in the pool in dollars is:

0.707 * 200 + 141.421 = 282.821

Using this value, you can calculate inconsistent losses from this example:

300 – 282.821 = 17,179

17,179/300 ≈ 0.0572 ≈ 5.72%

17,179 DAI or about 5.72% – this is what we would receive by simply storing assets instead of placing them in the pool. The profit from the initial position of 200 DAI was received, but it would be more profitable to simply store coins in the wallet.

A simple formula for calculating unstable losses:

Steering_USD/storage _USD – one

We apply the formula to our example:

282,821/300 -1 ≈ -0.0572 ≈ -5.72%

To determine the exact share in the bullet (in each token), you can use the formulas (2) and (3), the analytical platforms of the Uniswap Analytics and Sushiswap Analytics or third -party Croco Finance, Growing and Apy tools.Vision.

Why should the pool commission be taken into account?

In the previous example, trade commissions are excluded. Although this simplifies the calculation of inconsistent losses, the commission should be taken into account. They are an integral element of the AMM platform economy.

The larger the commission, the less inconsistent loss. When reaching a certain volume of trading fees, participation in the pool brings great profit than storage of assets.

Take the above example and add the component in the form of a commission:

We steak in the pool 1 ETH and 100 DAI;
The share of our steak is 10% (in the pool 10 ETH and 1000 DAI);
After a week, 1 ETH is traded for 200 DAI;
Commission fees: 1 ETH and 100 DAI.

Excluding trading commissions, an unstable loss is 17.179 DAI. Since the share in the pool is 10%, we have the right to 0.1 ETH and 10 DAI of the accumulated commissions. Since ETH is traded in 200 DAI, 0.1 ETH costs 20 DAI, and the total profit from the commissions is 30 DAI. Thus, the total amount is $ 312.821 ($ 282,821 + $ 30).

We will insert these new numbers into formula (4):

312,821/300 – 1 ≈ 0.042 ≈ 4.2%

In this example, a fickle loss is -12.821 DAI (17,179 -30). Thanks to the retention of assets in the pool instead of storage, this is not a loss, but an increase of 4.2%.

What is the formula for building a schedule of inconsistent losses?

A simple formula (4) was still used to calculate unstable losses. It is suitable for measuring the current IL, but uncomfortable if you need to get different values of unstable losses for different prices.

Of the formulas (1), (2) and (3), one more can be derived for the simplicity of calculating unstable losses:

We apply this formula to our example. We know that the initial r equal to 100 (1 ETH is traded for 100 DAI), and the final r equal to 200. Consequently, P equal to 0.5 (100/200). We use these values:

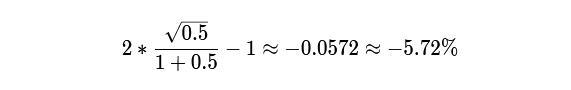
It was this number that we received by formula (4). Using this formula with different values P allows you to display IL at different prices.

This formula does not take into account the trade commission. If you need to build a schedule for trading commissions, the formula will be as follows:

You can calculate fees based on APY data that some AMM platforms provide.

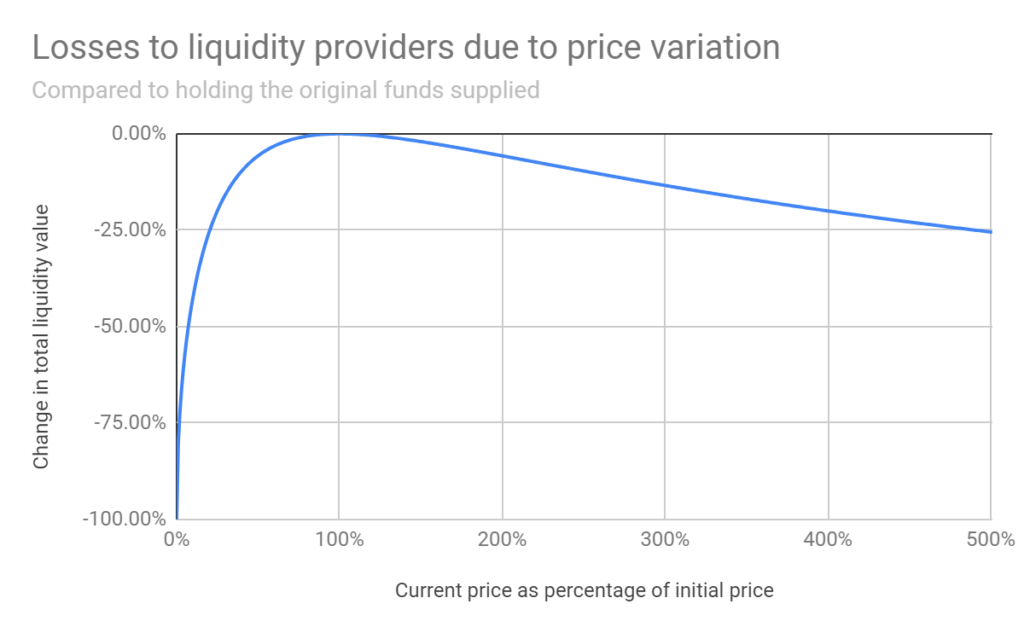
The schedule below illustrates inconsistent losses at various price changes. For example, a five -fold change in value entails il in 25.5%, double – 5.7%.

Is the mechanism of unstable losses in other pools works?

Curve is a decentralized exchange of stablecoins and tokenized bitcoins based on an automatic market maker mechanism. Its pools contain only assets that should have the same or comparable value: stablecoins (USDC, DAI) or tokenized bitcoins (Renbtc, WBTC). The risk of unstable losses in such pools is minimal.

Balancer offers pools with arbitrary ratios of tokens. For example, if a liquidity supplier wants to supply a large number of certain tokens, he can choose a pool in which these coins have a greater weight than others (proportions can be 80/20 or even 98/2). Such a model also minimizes an unstable loss. The larger the share of token in the pool, the less the difference in the results between the storage of token and the provision of liquidity in this token.

Bancor pools automatically change the specific gravity of tokens based on data reported by price oracles. Thanks to this, even in pools with volatile assets, you can minimize inconsistent losses.

How easy it is to calculate unstable losses?

Understanding unstable losses is necessary for any user of AMM platforms. You can make my own calculations IL using the calculator on the Dailydefi website.Org (the uniswap formulas are taken as a basis).

In general, users of AMM protocol are always subject to risks of the costs of missed benefit, regardless of the movement of prices. Compared to storage, if the prices of assets are growing, the position of the participant is growing not at such a high rate, if prices go down, he loses more.

Trade commissions and profitable farming come to the rescue-they help neutralize inconsistent losses so that participation in AMM-Pool brings great profit than simple storage of assets.